Swish method: differential expression accounting for inferential uncertainty

The Swish method, or "SAMseq With Inferential Samples Helps". Performs non-parametric inference on rows of y for various experimental designs. See References for details.

swish(
  y,
  x,
  cov = NULL,
  pair = NULL,
  interaction = FALSE,
  cor = c("none", "spearman", "pearson"),
  nperms = 100,
  estPi0 = FALSE,
  qvaluePkg = "qvalue",
  pc = 5,
  nRandomPairs = 30,
  fast = NULL,
  returnNulls = FALSE,
  quiet = FALSE
)

Arguments

y

a SummarizedExperiment containing the inferential replicate matrices of median-ratio-scaled TPM as assays 'infRep1', 'infRep2', etc.

x

the name of the condition variable. A factor with two levels for a two group analysis (possible to adjust for covariate or matched samples, see next two arguments). The log fold change is computed as non-reference level over reference level (see vignette: 'Note on factor levels')

cov

the name of the covariate for adjustment. If provided a stratified Wilcoxon in performed. Cannot be used with pair, unless using either interaction or cor

pair

the name of the pair variable, which should be the number of the pair. Can be an integer or factor. If specified, a signed rank test is used to build the statistic by default. Note: For simple paired designs, see use of fast=1 for a much faster implementation of paired testing using a one-sample z-score test statistic. All samples across x must be pairs if this argument is specified. Cannot be used with cov, unless using either interaction or cor

interaction

logical, whether to perform a test of an interaction between x and cov. Can use pair or not. See Details.

cor

character, whether to compute correlation of x with the log counts, and signifance testing on the correlation as a test statistic. Either "spearman" or "pearson" correlations can be computed. For Spearman the correlation is computed over ranks of x and ranks of inferential replicates. For Pearson, the correlation is computed for x and log2 of the inferential replicates plus pc. Default is "none", e.g. two-group comparison using the rank sum test or other alternatives listed above. Additionally, correlation can be computed between a continuous variable cov and log fold changes across x matched by pair

nperms

the number of permutations. if set above the possible number of permutations, the function will print a message that the value is set to the maximum number of permutations possible

estPi0

logical, whether to estimate pi0

qvaluePkg

character, which package to use for q-value estimation, samr or qvalue

pc

pseudocount for finite estimation of log2FC, not used in calculation of test statistics, locfdr or qvalue

nRandomPairs

the number of random pseudo-pairs (only used with interaction=TRUE and un-matched samples) to use to calculate the test statistic

fast

an integer (0 or 1), toggles different methods based on speed, currently only relevant for simple paired analysis. For simple paired design, fast=1 triggers the use of a one-sample z-score instead of a signed rank statistic. The one-sample z-score is much faster (can be >10x faster), by avoiding the expensive re-computation of ranks during permutations. fast=1 is not relevant for interaction or cor type designs

returnNulls

logical, only return the stat vector, the log2FC vector, and the nulls matrix (default FALSE)

quiet

display no messages

Value

a SummarizedExperiment with metadata columns added: the statistic (either a centered Wilcoxon Mann-Whitney or a signed rank statistic, aggregated over inferential replicates), a log2 fold change (the median over inferential replicates, and averaged over pairs or groups (if groups, weighted by sample size), the local FDR and q-value, as estimated by the samr package.

Details

interaction: The interaction tests are different than the other tests produced by swish, in that they focus on a difference in the log2 fold change across levels of x when comparing the two levels in cov. If pair is specified, this will perform a Wilcoxon rank sum test on the two groups of matched sample LFCs. If pair is not included, multiple random pairs of samples within the two groups are chosen, and again a Wilcoxon rank sum test compared the LFCs across groups.

References

The citation for swish method is:

Anqi Zhu, Avi Srivastava, Joseph G Ibrahim, Rob Patro, Michael I Love "Nonparametric expression analysis using inferential replicate counts" Nucleic Acids Research (2019). https://doi.org/10.1093/nar/gkz622

The swish method builds upon the SAMseq method, and extends it by incorporating inferential uncertainty, as well as providing methods for additional experimental designs (see vignette).

For reference, the publication describing the SAMseq method is:

Jun Li and Robert Tibshirani "Finding consistent patterns: A nonparametric approach for identifying differential expression in RNA-Seq data" Stat Methods Med Res (2013). https://doi.org/10.1177/0962280211428386

Examples

library(SummarizedExperiment)
set.seed(1)
y <- makeSimSwishData()
y <- scaleInfReps(y)
y <- labelKeep(y)
y <- swish(y, x="condition")

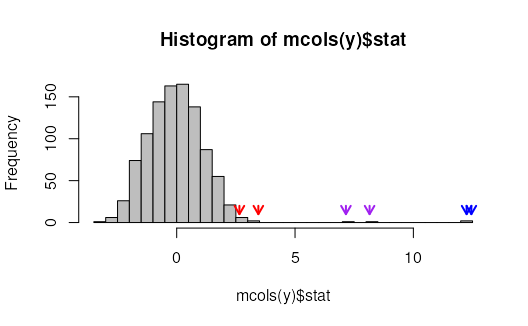
# histogram of the swish statistics
hist(mcols(y)$stat, breaks=40, col="grey")
cols = rep(c("blue","purple","red"),each=2)
for (i in 1:6) {
  arrows(mcols(y)$stat[i], 20,
         mcols(y)$stat[i], 10,
         col=cols[i], length=.1, lwd=2)
}


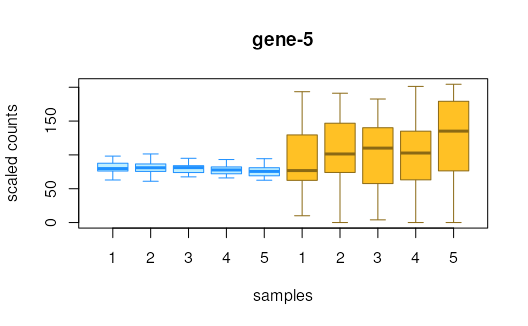
# plot inferential replicates
plotInfReps(y, 1, "condition")

plotInfReps(y, 3, "condition")

plotInfReps(y, 5, "condition")